4/6 데이터 구조 및 알고리즘 소개

알고리즘 이란?

Alogorithm은 어떠한 문제를 해결하기 위한 일련의 절차를 공식화한 형태를 표현한 것!!

데이터를 정리하여 효율을 만들어내는 것!! 

 

데이터란?

모든 분석 혹은 활용가능한 디지털화된 자료이자 정보!!

 

 

정렬 알고리즘

정렬 알고리즘은 여러 방식이 있는데 주어진 문제에 따라 알고리즘을 선택한다. 이때 고려해야 할 사항은 시간 복잡도와 공간 복잡도이다. 시간 복잡도는 알고리즘이 결과를 도출하는데 걸리는 시간 값이고 공간 복잡도는 알고리즘이 결과를 도출하는데 필요한 공간의 값이다.

따라서 최적의 알고리즘은 가장 빠르고 가장 작은 공간을 사용하는 알고리즘이다.

 

 

일단 시작하기 전에 Stable 정렬과 In-place 정렬에 대해 알고 있자.

 

Stable 정렬

정렬 했을 때 중복된 값들의 순서가 변하지 않는 것을 말한다.

예시)

arr = [1, 7(1), 3, 5, 4, 7(2), 9] 을 정렬했을 때

• arr = [1, 3, 4, 5, 7(1), 7(2), 9] 이면 Stable(안정)

• arr = [1, 3, 4, 5, 7(2), 7(1), 9] 이면 Unstable(불안정)

In-place 정렬

정렬하는데 추가적인 메모리 공간이 거의 들지 않는 것을 말한다. (제자리 정렬)

 

 

1. Selection Sort, 선택 정렬

 

선택 정렬은 데이터 중 가장 작은 값의 데이터를 선택하여 앞으로 보내는 정렬 방법이다. 

비열에서 최솟값을 찾아야 하기 때문에 비교 횟수는 많지만 교환 횟수는 적다는 특징이 있다.

• 주어진 배열에서 가장 작은 최솟값을 찾고 배열의 맨 앞의 값과 위치를 바꾸면서 정렬한다.
• 맨 앞의 값을 제외한 배열로 끝날때 까지 반복한다. 

시간 복잡도

• (n-1) + (n-2) + .... + 2 + 1 = n(n-1) / 2 이므로 시간 복잡도는 O(n^2) 입니다.

• 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일합니다.

장점

• 구현이 간단하다.
• 많은 교환이 일어나야 하는 자료상태에서 비교적 효율적이다.
• 정렬하고자 하는 배열 안에서 교환하는 방식이므로 In-place 정렬이다.

단점

• 데이터를 하나씩 비교하기 때문에 비효율적이다.
• Unstable 정렬이다. (구현하는 방식에 따라 달라질 수 있다.)
• 정렬된 상태에서 새로운 데이터가 추가되면 정렬 효율이 좋지 않다.

2. Bubble Sort, 거품 정렬

버블 정렬은 첫번째 원소부터 인접한 원소와 비교하며 자리를 바꾸면서 맨 끝부터 정렬하는 방식이다. 정렬 방식이 물속에서 올라오는 물방울 같다고 해서 버블정렬이라 한다.

 

 

시간 복잡도

• (n-1) + (n-2) + .... + 2 + 1 = n(n-1) / 2 이므로 시간 복잡도는 O(n^2) 입니다.

• 항상 2개의 원소를 비교하기 때문에 최선, 평균, 최악의 경우 모두 시간복잡도가 O(n^2) 으로 동일합니다.

장접

• 구현이 간단하고, 소스코드가 직관적이다.
• 정렬하고자 하는 배열 안에서 교환하는 방식이므로 In-place 정렬이다.
• Stable 정렬이다.

단점

• 시간 복잡도는 별로다. 굉장히 비효율인 편이다.
• 데이터를 하나씩 비교하기 때문에 비교 횟수가 많아지므로 시간이 오래걸린다.
• 정렬된 상태에서 새로운 데이터가 추가되면 정렬 효율이 좋지 않다. 

 

3. Insertion Sort, 삽입 정렬

버블 정렬의 비효율성을 개선하기 위해 등장한 방법이다. i 번째 원소를 정렬된 상태의 앞부분과 비교하여 적절한 위치에 삽입하는 방식이다. 버블 정렬의 비교 및 교환 횟수를 줄여 높은 효율을 보여준다. 

 

• i-1 번째 원소까지 모두 정렬된 상태여야 하고 i-1부터 0번째까지의 원소와 i번째 원소를 각각 비교한다. 
• 이때 i 번째 원소보다 작은 값이 발견된다면 그 위치에 i 번째 원소를 삽입한다. 

시간 복잡도

• 최악의 경우(역으로 정렬되어 있을 경우), (n-1) + (n-2) + .... + 2 + 1 = n(n-1 )/ 2 으로 O(n^2) 이다.
• 하지만 모두 정렬이 되어있는 경우, 한번씩 밖에 비교를 안하므로 O(n) 의 시간복잡도를 가지게 된다.
• 최선 = O(n), 평균과 최악 = O(n^2)이다.

장점

• 입력으로 들어오는 배열의 원소가 정렬되어 있을수록 속도가 빠르다.
• 정렬된 값은 교환이 일어나지 않는다.
• 이미 정렬되어 있는 배열에 자료를 하나씩 삽입/제거하는 경우, 최고의 정렬 알고리즘이 된다.
• 정렬하고자 하는 배열 안에서 교환하는 방식이므로, In-place정렬이다.
• Stable 정렬이다.
• 선택정렬, 버블 정렬과 비교했을 때 상대적으로 빠르다.

단점

• 평균과 최악의 시간복잡도는 O(n^2)로 비효율적이다.
• 선택, 버블 정렬과 마찬가지로 배열의 길이가 길수록 비효율적이다.

4. Quick Sort, 퀵 정렬

 

 

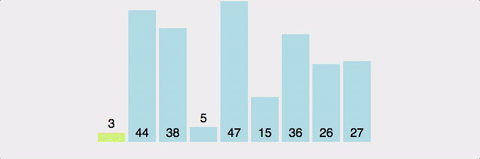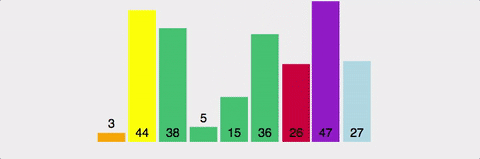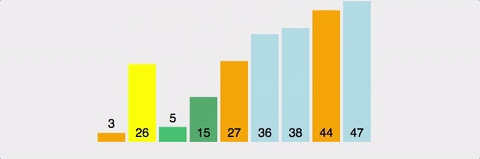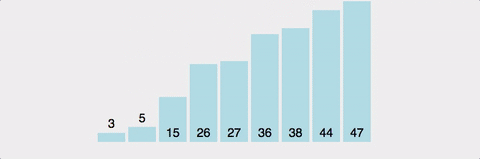
분할 정복(divide and conquer) 방법을 통한 정렬로, 하나의 pivot(축)을 정해서 이 pivot보다 작은 값은 왼쪽에 큰값은 오른쪽에 위치시키는 방법이다.

 

• 왼쪽과 오른쪽에 해당하는 원소들에 대해 두 배열로 나눈다. -> 분할(Divide)
• 분할된 두 개의 작은 배열에 대해 재귀(Recursion)적으로 이 과정을 반복한다. 
• 재귀 호출이 한번 진행될 때마다 최소한 하나의 원소는 최종적으로 위치가 정해지므로, 이 알고리즘은 반드시 끝난다는 것을 보장할 수 있다.

시간 복잡도

• 최선과 평균의 경우 O(nlogn)이다.
• 최악의 경우(정렬되어 있는 경우) O(n^2)이다.

장점

• 불필요한 데이터의 이동을 줄이고 먼 거리의 데이터를 교환한다.
• 한 번 결정된 pivot들이 추후 연산에서 제외되는 특성 때문에, 시간 복잡도 O(nlogn)을 가지는 다른 정렬 알고리즘과 비교했을 때 가장 빠르다.
• 정렬하고자 하는 배열 안에서 교환하는 방식이므로 In-place 정렬

단점

• 정렬된 배열에 대해서는 불균형 분할에 의해 오히려 수행시간이 더 많이 걸립니다.
• Unstable 정렬입니다. 

 

이외에도 힙, 계수, 병합 정렬이 있단다. 나중에 봐야겠다. 

 

내가 참고한 형님들이다. 많이 똑똑하시다. 

 

https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html

[알고리즘] 선택 정렬(selection sort)이란 - Heee's Development Blog

https://east-star.tistory.com/10#%EC%84%A0%ED%83%9D%20%EC%A0%95%EB%A0%AC(Selection%20Sort)-1

정렬 알고리즘(Sorting Algorithm) 정복하기 - with JS